阅读笔记:Fine-grained air pollution inference with mobile sensing systems: A weather-related deep autoencoder model
一、基本信息
- 阅读人和日期:XW Guo,2022.3.18
- 引用格式:Rui Ma, Ning Liu, Xiangxiang Xu, Yue Wang, Hae Young Noh, Pei Zhang, and Lin Zhang. 2020. Fine-Grained Air Pollution Inference with Mobile Sensing Systems: A Weather-Related Deep Autoencoder Model. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 4, 2, Article 52 (June 2020), 21 pages. https://doi.org/10.1145/3397322
- 原文链接:https://dl.acm.org/doi/abs/10.1145/3397322
- 概述:除了静态的中央空气质量监测站外,城市空气污染监测还部署了移动传感系统,以实现更细的传感覆盖范围和更大的采样粒度。然而,数据的稀疏性和不规则性也给污染地图的恢复带来了巨大的挑战。为了解决这些问题,本文提出了一种基于深度自动编码器框架的推测算法。在该框架下,将由不规则样本构成的部分观测污染地图输入到模型中,然后由编码器和解码器共同工作来恢复整个污染地图。在解码器内部,采用卷积长短时记忆(ConvLSTM)模型,将大气扩散模型作为其物理解释,并进一步提出与天气相关的ConvLSTM,以实现准实时应用。
二、动机及创新点
动机:
- 深度学习方法的不可解释性:没有物理洞察力的深度学习模型可能具有很差的外推能力;
- 来自移动感知的不规则样本:在现有的机器学习结构上,很难直接用来自移动感知的不规则样本来建模时空邻域中的依赖关系。
主要贡献及创新点:
- 提出一个细粒度空气污染推断的自动编码器框架,可应用于任何形式的不规则观测。
- 用卷积长短时记忆(ConvLSTM)结构模拟空气污染演变过程,并揭示其在重新制定的大气扩散模型下的物理解释。通过开发与天气相关的ConvLSTM(wr-ConvLSTM)来实现准实时推理,该模型将每日的ConvLSTM模型与同步的天气信息连接起来。
- 在真实世界的空气污染传感系统上评估提出的算法。比较了现有方法在离线应用和准实时应用中的性能。
三、问题描述和方法论
1. 估计完整的污染地图
由于目标$\Phi$和给定观测地图$\Phi_{obs}$在同一时间和空间范围内,这个问题也可以看作是一个插值或外推问题。实际上是在稀疏的观测地图条件下逼近真实的污染地图,求解的是一个条件概率问题。
$$
\widetilde{\Phi}=\arg{\max{P\left(\left.\Phi\right|\Phi_{obs}\right)}}
$$
2. 自动编码器框架
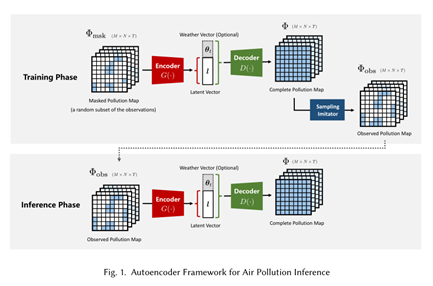
部分观测的污染地图是编码器的第一个输入。编码器降低观测的维数,并将其压缩为隐向量l。然后,我们可以选择将该向量连接到表示天气相关信息的辅助向量$\theta_t$(根据编码器输入的要求),并将其提供给解码器。解码器充当“污染场生成器”,输出代表完整空气污染地图的三维矩阵$\widetilde{\Phi}$。
1) 训练阶段
为了学习编码器和解码器中的参数,在训练阶段需要另一个模块,采样模拟器。它在重构的污染地图上模拟移动传感系统的传感行为,从而得到一个“重构”的观测矩阵${\widetilde{\Phi}}_{obs}$。通过将“重构”的观测矩阵${\widetilde{\Phi}}_{obs}$与真实观测矩阵$\Phi_{obs}$进行比较,评估编码和解码的性能,以便对编码器和解码器进行训练。
在训练阶段,我们随机选择一个子集,以固定百分比作为输入样本,进行特定次数的观察。因此,我们获得了一个特定数量的“掩码污染地图”,每个掩码污染地图都随机覆盖了与模型输出相对应的“观测污染地图”。每个输入样本随机覆盖输出样本,因此自动编码器学习输出矩阵不同元素的值外推。
2)推测阶段
在推测阶段,将“观测污染地图”输入到训练好的框架中,然后将输出视为我们的目标污染地图
3. 具有物理洞察力的天气相关ConvLSTM(wr-ConvLSTM)
1) 对流扩散污染传播模型
根据大气理论,大气扩散过程可以用对流扩散方程来描述:
$$
\frac{\partial P}{\partial t}=\mathrm{\nabla}\cdot\left(k\mathrm{\nabla p}\right)-\mathrm{\nabla}\cdot\left(\nu_P\right)+s
$$
式中,$P[kg/m ^3]$是污染物浓度,$t[s]$是时间。污染物浓度随时间的变化是右侧三个因素的总和:1)扩散、2)对流、3)数量的产生或破坏。这里,$v[m/s]$是风速矢量,$S[kg/m^3s]$是指示源位置和排放率的源项,$k[m^2/s]$是表示扩散系数的对角矩阵,其项为 湍流涡流扩散系数(turbulent eddy diffusivities)。
离散时空坐标[i, j, k](对应于空间的x轴、y轴和时间的t轴)处的污染物浓度可以通过时间k-1处一组局部邻域的浓度来确定:
$$
\begin{split}P\left[i,j,k\right] = &a_1 \left[i,j,k\right]\cdot P\left[i,j,k-1\right]+a_2\left[i,j,k\right]\cdot p\left[i-1,j,k-1\right]+ \\
&a_3\left[i,j,k\right]\cdot p\left[i+1,y,k-1\right]+a_4 \left[i,j,k\right]\cdot p\left[i,j-1,k-1\right]+ \\
&a_5\left[i,j,k\right]\cdot p\left[i,j+1,k-1\right]+s\left[i,j,k\right]\end{split}
$$
可以写成F-范数的形式:
$$
P\left[i,j,k\right]=\left\langle A\left[i,j,k\right]\cdot Q\left[i,j,k\right]\right\rangle_F+s\left[i,j,k\right]
$$
其中,
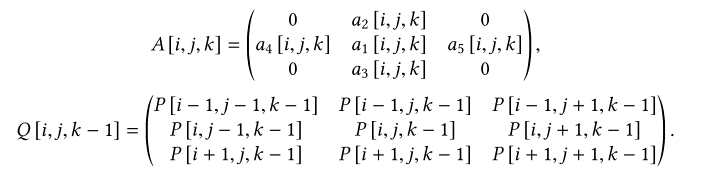
在空间均匀性假设下,即某个时间k的扩散系数K和风速v在每个[i, j]上是恒定的,系数矩阵A在整个空间M×N上是恒定的。那么,在时间k上,M×N空间上的污染表示为:
$$
p_k=p_{k-1^\ast}A_k+S_k \qquad(7)
$$
式中,*表示卷积操作。此物理模型估计的污染可能受累积误差的影响,原因如下:
a)描述离散化$P_{k-1}$和$P_{k}$之间的转换,使用线性模型可能不够充分;
b)对模型系数的不准确了解:K值的选择通常是经验的,s是人工调查收集的。
由于确定性的物理模型存在这些缺点,本文提出用ConvLSTM(本文框架的解码器结构)来替代它,并给出了物理解释:
对于一个空间区域上的动态系统,公式(7)正是简单的ConvLSTM(没有激活层)所做的事。它描述了状态$P_{k-1}$如何随时间变化为$P_{k}$,其中$A_k$对应于转换内核(卷积核),$S_k$对应于偏差矩阵。与确定性模型(7)相比,ConvLSTM涉及更多参数和非线性表达,以捕获详细信息,从而弥补由a)引起的误差。这些参数是从数据中学习的,因此它们在当前场景中更准确,并且不受b)中预设的不准确参数的影响。
2)在离线应用中使用具有物理洞察力的普通ConvLSTM对流扩散污染传播模型
普通的ConvLSTM:
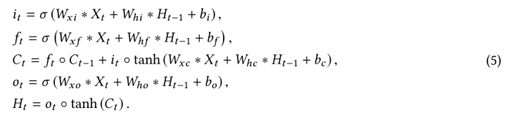
式中,*表示卷积操作。一般的LSTM有四个隐藏的全连接层,把它们全部换成卷积层就变成了ConvLSTM,也即使用卷积操作来代替矩阵乘法操作。
3)使用wr-ConvLSTM实现准实时应用
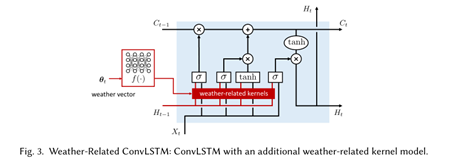
wr-ConvLSTM:
假设污染扩散在一天内遵循一个参数相同的模型,我们为每一天建立单独的模型。为了将该方法应用于准实时空气污染推断,即模型不需要使用新数据进行训练,在具有辅助天气信息的日常模型之间建立了连接。具体而言,在ConvLSTM中,预计将在输出层获得污染浓度,即公式(5)中的$H_t$。考虑气象、地理和POI信息对污染浓度估计的影响,ConvLSTM中与之相关的卷积核可建模为:
$$
w_{hi},w_{hf},w_{hc},w_{ho}=f\left(\theta_k\right)
$$
其中,$\theta_k$表示一个向量,包含时间k的气象、地理和POI信息。然后我们采用全连接神经网络来描述$f(\bullet)$。
四、实验部分
1. 数据集
数据集包含两部分:来自分布式传感器网络的空气污染记录 [1],来自官方气象站的气象参数 [2]。
2.基线方法
全连接神经网络(ANN)、逆距离加权插值(IDW)和高斯过程回归(GPR)。
3. 评价指标
均方根误差(RMSE)、平均绝对误差(MAE)和皮尔逊相关系数(CORR)。
4. 实验结果
不同离线方法的性能对比,结果如下表所示:
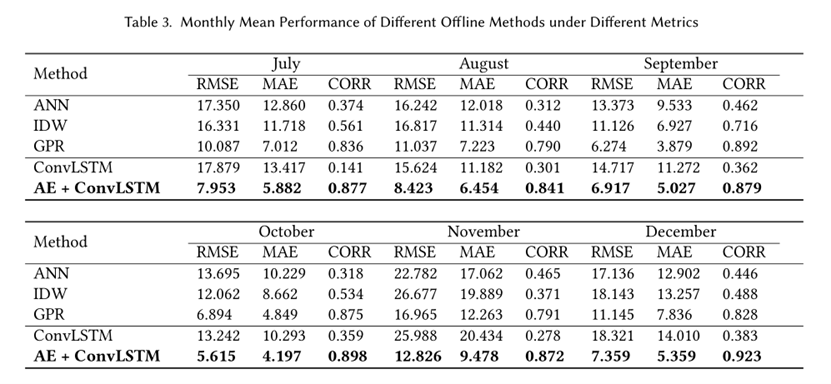
不同准实时方法的性能对比,结果如下表所示:
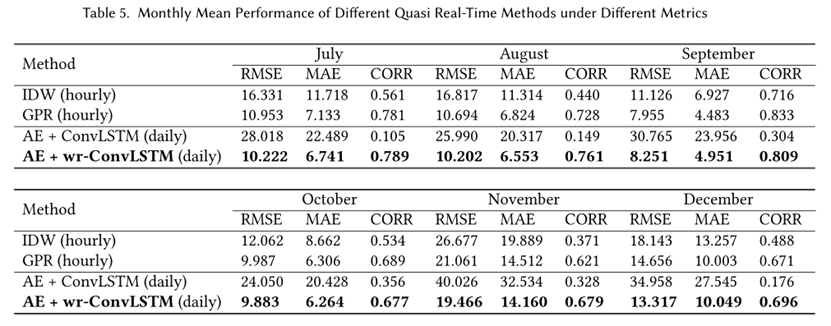
[1] https://drive.google.com/file/d/1hdiYt3scAI0hxlvuGLBYoZzlWjZFNPat/view?usp=sharing
