阅读笔记:Towards Robust Task Assignment in Mobile Crowdsensing Systems
一、基本信息
- 阅读人和日期:SY Chen,2022.3.4
- 引用格式:Wang, L., Yu, Z., Wu, K., Yang, D., Wang, E., Wang, T., Mei, Y. & Guo, B. (2022). Towards Robust Task Assignment in Mobile Crowdsensing Systems. IEEE Transactions on Mobile Computing.
- 单位:Northwestern Polytechnical University.
- 原文链接:https://ieeexplore.ieee.org/document/9713668/
- 概述:论文在移动群智感知系统的离线任务分配过程中考虑鲁棒性,将任务分配问题形式化为双目标优化问题,通过利用工人的时空移动性和进化的多任务范式,作者提出了一种基于分配图的方法-EMTRA,包括构建分配图和基于人口的进化计算两个阶段。目标是增强离线任务分配方案的鲁棒性的同时,最小化工人的绕行成本。
二、动机及创新点
动机:
在群智感知系统的实际任务执行过程中,会存在各种不可预知的中断,比如参与者放弃完成任务、设备故障等,这就可能导致任务执行失败。然而,实时改变预定的分配方案,即重新开发分配方案又难免牺牲系统性能。因此,论文提出了一种解决方案,即主动创建一个鲁棒的离线任务分配方案。
主要贡献及创新点:
- 首次在移动群智感知系统的任务离线分配过程中考虑鲁棒性。
- 将问题表述为一个双目标优化问题,目标是最小化招聘工人的绕行成本,同时最大化分配方案的鲁棒性。通过利用工人的时空流动性和进化的多任务范式,提出了一种基于分配图的方法来解决问题。
- 对两个现实数据集进行了广泛的实验,并展示了方法的有效性和实用性。
三、问题描述和方法论
1. 问题描述
作者将 MCS 中的鲁棒任务分配 (RBTA) 问题形式化为双目标的多任务优化问题。目标是在最小化参与者的绕行成本的同时,最大化分配方案的鲁棒性。具有鲁棒性的方案会比不易调整的最优方案更有价值。因此,我们必须全面搜索整个搜索空间,并获得足够多的帕累托最优分配方案。不仅需要通过匹配任务的要求和参与者的特征(例如移动路线和所具备的能力)开发预分配方案,还需要针对任务执行过程中的潜在中断进行多次重新分配测试。在模拟仿真实验中,有必要反复进行模拟参与者的移动轨迹,并沿着任务的执行过程动态地重新规划他们的移动路线。
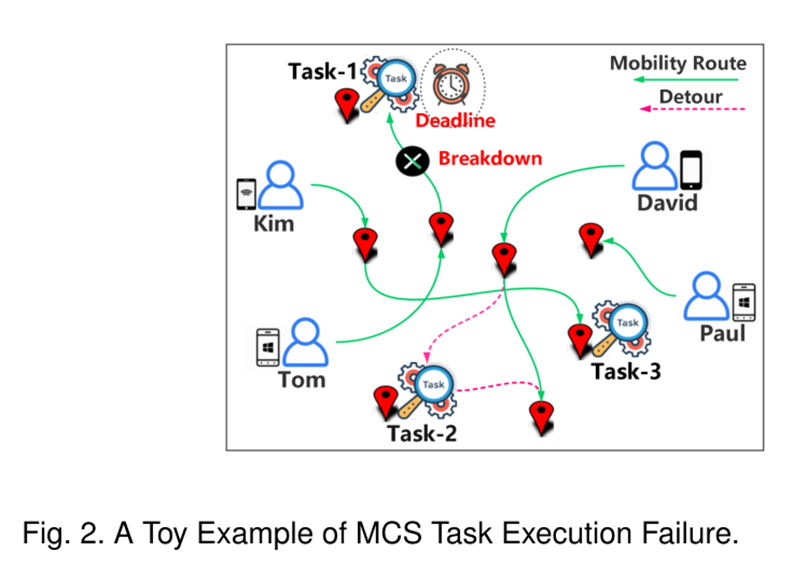
如图所示,事先选择Tom执行任务1,若在执行过程中发生故障,则没有可用的参与者来接管任务1,尤其是当它接近任务的最后期限时,任务大概率无法完成。
问题形式化描述
任务:
$$ \mathcal{T}=\left\{t_{1},t_{2},\ldots,t_{n}\right\} $$参与者:
$$ \mathcal{U}=\left\{u_{1},u_{2},\ldots,u_{m}\right\} $$分配方案:
$$ \mathcal{S}=\left\{\left(t_{i},u_{j}\right)\mid t_{i}\in\mathcal{T},u_{j}\in\mathcal{U}\right\} $$鲁棒性指标:
$$ \operatorname{RBS}(\mathcal{S})=\frac{\frac{1}{N} \sum_{x=1}^{N} \sum_{u_{j} \in \mathcal{S}_{x}^{*}} \operatorname{TD}\left[\operatorname{Rt}\left(u_{j}\right), \operatorname{Rt}^{*}\left(u_{j}\right)\right]-\operatorname{TD}(\mathcal{S})}{\operatorname{TD}(\mathcal{S})} $$原方案总的绕行成本:
$$ \operatorname{TD}(\mathcal{S})=\sum_{u_{j}\in\mathcal{S}}\operatorname{TD}\left[\operatorname{Rt}\left(u_{j}\right),\operatorname{Rt}^{*}\left(u_{j}\right)\right] $$双目标优化问题:
目标函数:
$$ \left\{\begin{array}{lc}\min:&\sum_{u_{j}\in \mathcal{S}}\operatorname{TD}\left[\operatorname{Rt}\left(u_{j}\right),\mathrm{Rt}^{*}\left(u_{j}\right)\right],\\ \min:&\frac{\frac{1}{N}\sum_{x=1}^{N}\sum_{u_{j}\in\mathcal{S}_{x}^{*}}\operatorname{TD}\left[\operatorname{Rt}\left(u_{j}\right),\mathrm{Rt}^{*}\left(u_{j}\right)\right]-\operatorname{TD}(\mathcal{S})}{\operatorname{TD}(\mathcal{S})}\end{array}\right. $$约束条件:任务-参与者的条件匹配和任务的DDL
$$ \mathcal{S}=\left\{\left(t_{i},u_{j}\right)\mid u_{j}\in\mathrm{Cu}\left(t_{i}\right)\wedge\mathrm{AT}_{t_{i},u_{j}}+\mathrm{Et}\left(t_{i}\right)\leqslant\mathrm{Dl}\left(t_{i}\right)\right\},t_{i}\in\mathcal{T}\text{and}u_{j}\in\mathcal{U} $$2. 构建任务分配图
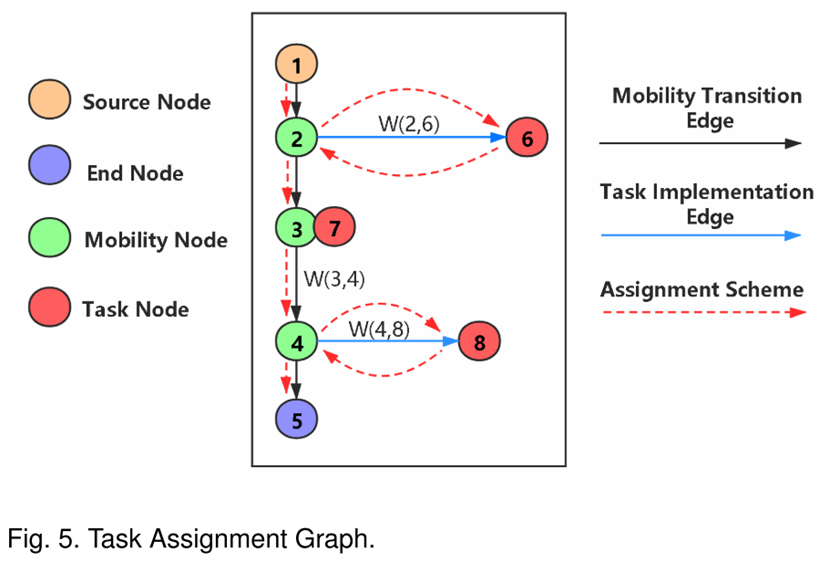
任务分配图中包括后续需要用到的信息:绕行成本和时间余量。算法及任务分配图如下:

3. 基于种群的进化算法——EMTRA
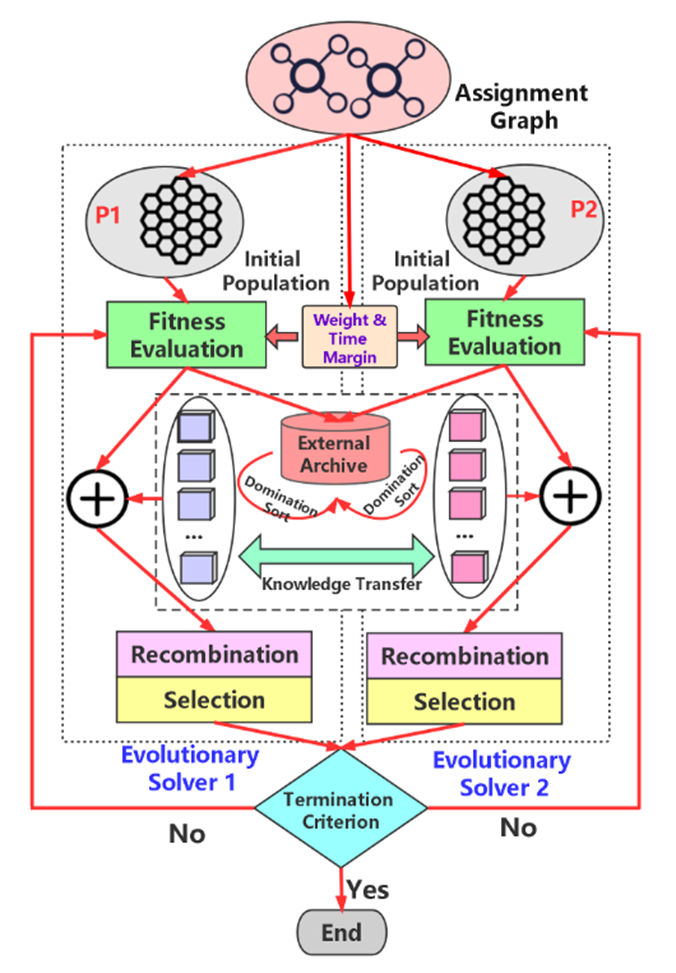
EMTRA是基于18年论文《Evolutionary Multitasking via Explicit Autoencoding》通过显式自编码器的进化多任务优化方法提出的。相比较单目标优化算法,只输出一个分配方案,EMTRA将返回一组 Pareto 分配方案,它可以全面揭示所有最优分配方案,在绕行成本和鲁棒性指标之间进行不同的权衡——目的就是要找到足够多的帕累托最优分配方案。

下图分别为进化求解器1和2生成两个不同的种群 P1 和 P2。 并且在进化生成过程中,求解器 1 和求解器 2 分别用种群 P1 和 P2 独立处理它们的子问题,即最小化绕行成本和最小化鲁棒性指标。 此外,建立了一个外部档案来记录所需的帕累托解,即在每一代进化中发现的一组非支配解。 通过利用帕累托解,知识在 P1 和 P2 之间转移,将优化器引导到更有希望的解决方案。 在进化过程中,执行重组和选择操作以产生后代方案,从而提高各自的目标。 该过程一直进行,直到达到给定的终止标准。 迭代结束后,将当前存储在外部存档中的解决方案确定为最终输出结果。